Truly Tricky Graduate Physics Problems

For a long time, my collection of Physics problems has been one of the largest draws on my website.  Now, many of my favorite graduate Physics problems are available in an e-book from Bitingduck Press, Truly Tricky Graduate Physics Problems.  

The solutions that have previously been available here are still available for free, and always will be.  I find them helpful as a reference and wanted them to be available to others as well.  The solutions in the book include my own favorite problems as well as new problems from the other authors, Jay Nadeau and Leila Cohen, and are written in a format that can easily be cut-and-pasted into your favorite computer algebra system.

If you've found my Physics problem collection helpful in preparing for your qualifying exams, you may want to check out the e-book as well for more challenging Physics problems to help you prepare.

Pinhole Picture from Arizona

Last January, I hid 5 pinhole cameras in the desert near Phoenix, AZ with the goal of taking some stunning pinhole photographs, taking advantage of the bright desert sun and the reflective desert sand.  In order to ensure that they wouldn't be found, we pulled over at a random place along N. Bush Highway, walked about 50 feet in the desert, and plastic tied the cameras to stumps or desert flora.

I still think it was a pretty solid plan, but there were a few flaws.  First, the desert in Arizona gets so hot that even the photo paper doesn't want to deal with it.  It looks like after only a month or two of hot days, the photo paper curled up in the oven-like can and completely stopped exposing.  Second, my estimation of how much light reflects off the sand was pretty far off.  The parts of the image that looked at sand were just dark and indistinct.  The simple fact is that the sun is so bright that everything else may as well be black.  Third, it turns out that the desert there must see more pedestrian traffic than I expected.  One of my cameras was totally destroyed, and one had been torn open and the photo paper taken out.

The one shot that came out all right was less than ideal.  I had placed the can horizontally and facing East on the theory that I would get reflections of the sunrise off of the desert sand, and that the sunrises over Four Peaks would give a striking horizon.  I guess it sort of worked, except that the desert was nothing distinct and Four Peaks was partially obscured by some desert plants.

Sunrise over Four Peaks in Arizona.  Thanks to the Christoph family for helping me to place and retrieve this photo!  Placed Jan. 5, 2013, retrieved Nov. 9, 2013.  Film curled up in the can, so it was not exposing for much of that time.

Diminishing Returns in the Game of Go

We've been playing a lot of Go at work lately.  Sometimes my mind wanders as I play, and I see parallels to life in the board positions.  Arguments, negotiations, trades, consensus, squabbling, greed and fear.

The goal of Go is to surround as much territory using your stones as possible.  So, if at all possible, players should try to place stones in such a way as to grab the most area first, and then leave small amounts of area, just a few points, for last.  The game ends either when one player surrenders or when both players feel that the remaining moves are worth zero points or less.  I wonder:  what does the rate of diminishing returns look like in Go?  How much is the first move worth versus the second?  The tenth?  the hundredth?  Knowing this will help me understand when it might be worth it to walk away from a battle versus to keep fighting it at each stage of the game.

As a secondary goal, I'd like to evaluate komi.  Komi is an amount of points granted to the white player to offset the disadvantage of going second.  Ideally, the komi should be set such that if both players played perfectly, then black's score would exactly equal white's score.  If Go is to be a fair game, then if I assigned each move m a point value V(m) and that black and white took turns making M moves in a game without passing, I would expect that

Equation 1:  Calculation of komi using V(m), the point value of the m-th move in a game of Go.  M is the number of moves in an ideal, perfect game, and it is assumed that no player pass during play.

I will use GNU Go and the Go Text Protocol to evaluate a freely available collection of Go games from Andries Brouwer, and also to generate a set of computer games where GNU Go plays itself.  After each move, I will ask GNU Go to run evaluate_score and see how the score has changed from the previous move.  I posit that this difference is an estimate for V(m) in the equation above.

I used this python script to generate the simulated games.  I then produced a box and whisker plot for the calculated V(m) for each move using the following bash commands:

# Get all deltas. cat all-sims | awk '{print $2, $3}' > generated-files/delta-vs-move # Produce box and whisker plots for each move. cat generated-files/delta-vs-move | sort -k 1 -gk 2 | awk 'BEGIN {n=0;l=1} ($1==l) {a[n]=$2;n+=1} ($1!=l) {print l, a[int((n-1)/2)], a[int(3*(n-1)/4)], a[int((n-1)/4)], a[n-1], a[0];n=1;l=$1;a[0]=$2} END {print l, a[int((n-1)/2)], a[int(3*(n-1)/4)], a[int((n-1)/4)], a[n-1], a[0]}' > generated-files/simulated-box-and-whisker

Plotting using xmgrace tells a pretty cool story:

Figure 1:  Value of moves in go V(m) calculated using 5000 games simulated by GNU Go on a 19 by 19 board.  Score estimates come from GNU Go's built in estimate_score function.

There are several important messages to take from Figure 1.  First, as demonstrated by the narrow interquartile range shown in blue, that typical moves in Go have a value that is closely related to the move number.  Second, we see that Go is also a game of tactics where particular tactical situations can be responsible for wild fluctuations in the score.  Very good tactical moves account for the extreme high move values, and very poor moves account for the extreme low move values.  This plot also underscores the point of my study:  when it is a good idea to simply walk away from a battle and play elsewhere.  Clearly, if I believe that a battle is worth 20 or more points, I should always fight it according to this plot.  Below that, the story becomes more interesting.

Figure 2:  This is identical to Figure 1, but rescaled and with the whiskers removed from the box and whisker plot.  Note that the IQRs did not include moves with values less than zero, and nothing is hidden below the x-axis.

Figure 2 shows a different view of the simulated data in Figure 1.  The interquartile range shows the values of typical moves in Go.  The median value of the first move of the game is 10.4 points.  The median value of the tenth is 7.3,  the fiftieth is 4.9, the hundredth is 2.8, and the hundred-fiftieth is 1.3.  These figures give me an idea of the immediate value of sente, or when it may be worthwhile to simply ignore the opponent's last move and play elsewhere.

Next, I wonder if Equation 1 allows me to reconstruct Komi.  A simple command line allows me to perform the calculation:

cat simulated-box-and-whisker | awk '{print $4}' | awk 'BEGIN {t=0} (NR % 2 == 0) {t -= $1} (NR % 2 == 1) {t += $1} END {print t}' -0.3

This estimate is not even close to GNU Go's default Komi, 5.5.  This reveals a limitation of my study:  while most moves' values fall in a narrow interquartile range, no game is composed entirely of typical moves shown in Figure 2.  Victory lies not in these average moves, but instead in the long tail of outliers visible in Figure 1 (green extremes).

Now let's try this experiment again with 5000 human games.  I will start with the empty board, then after each turn ask GNU Go to evaluate the new value of the board.  The difference between the previous board value and the next will be called the value of each move.

Figure 3:  Value of moves in go V(m) calculated using even human games by GNU Go on a 19 by 19 board.  Score estimates come from GNU Go's built in estimate_score function.

Figure 3 looks vaguely reminiscent of Figure 1, but with a glaring difference:  the value of the moves in the mid-game actually seems to be greater than the value of the early game moves!  Let's take a closer look at this by focusing on the interquartile range.

Figure 4:  This is identical to Figure 3, but rescaled and with the whiskers removed from the box and whisker plot.  Note that the IQRs did not include moves with values less than zero, and nothing is hidden below the x-axis.

Comparing Figure 4 to Figure 2, it becomes clear that there is something profoundly different between the human games and the AI games.  The GNU Go-predicted point value of moves remains high, around 10 stones on average, out to the hundredth move.  Further, the interquartile range is much broader and skewed towards more valuable moves.  So, what's going on here?

First, consider that most of the human games end in resignation.  None of the GNU Go games end in resignation.  So, what do human players do when they feel that they are losing lost that GNU Go does not?  They try a hail Mary.  They make an exceptionally risky move that, while likely to fail, may put them back in the game.  If this risk fails, a human player will probably resign.

Figure 5:  Human games tend to be shorter than GNU Go games, because GNU Go never resigns.  Before resigning, humans tend to make a big gamble that, should it succeed, is worth a significant number of points.  If aliens came to this planet and wanted to understand the difference between humans and computers, this would tell them all that they need to know.

Figure 5 shows us that human games tend to be shorter than GNU Go games due to resignation, and taken together with figures 3 and 4 we see that the losing player tends to make big gambles that are worth a lot of points if they succeed.  AI players, on the other hand, cannot transcend their heuristic algorithm.  They will make the move that they see as most profitable every time, whether they are ahead or behind.

Finally, I want to discuss exactly what the value of a move means.  Above, I have posited that the value of a move is the point value, in stones.  But, what if you don't care about points, and only care about winning or losing by any number of points?  The one point that puts you slightly ahead of your opponent, then, is worth more than 50 points that still leave you behind.

This is a difference between the Pachi algorithm and GNU Go.  GNU Go is concerned about values in stones, and Pachi is concerned about probability of winning.  Pachi, in fact, will resign if it cannot find any scenario in which it will win.  Pachi's Monte Carlo algorithm was a huge breakthrough in computer Go, but its skill on a 19 by 19 board is still a far cry from professional play.  A fun experiment is to use the sgf-analyze.pl script included with Pachi to track probability of winning through a game, and as such to identify the major plays and blunders of a game.

Pachi supposedly plays at a 2d level on KGS, which means that it is likely to have a hard time analyzing games by players at a higher level than 2d.

Out of curiosity, I tried runing sgf-analyze on a 9d game annotated by GoGameGuru.  I ran 1 million simulations per move using the extra pattern files, and ran analyze-sgf once for black and once for white.  The output of sgf-analyze looks something like this:

2, W, D16, C12, 0.52 4, W, D3, M17, 0.52 6, W, P3, R9, 0.52 ...

Sample output from Pachi's sgf-analyze.pl script.

./sgf-analyze.pl game.sgf B -t =1000000 threads=4 -d 0 dynkomi=none > analysis-B ./sgf-analyze.pl game.sgf W -t =1000000 threads=4 -d 0 dynkomi=none > analysis-W tail -n +2 analysis-B | tr -d "," | awk '($3 == $4) {print $1, $5}' > B-agree tail -n +2 analysis-B | tr -d "," | awk '($3 != $4) {print $1, $5}' > B-disagree tail -n +2 analysis-W | tr -d "," | awk '($3 == $4) {print $1, 1 - $5}' > W-agree tail -n +2 analysis-W | tr -d "," | awk '($3 != $4) {print $1, 1 - $5}' > W-disagree xmgrace -nxy B-agree B-disagree W-agree W-disagree

The output from sgf-analyze is easy to work with.  I used a procedure like this to generate the beautiful plot in Figure 6.
The first column is the move, the second column is the player color, the third is the move actually played, the fourth is the suggested move by Pachi, and the fifth column is the probability (according to Pachi) of this player winning assuming that he plays the recommended move. There is no doubt that these 9d players are much better than Pachi, so I'll assume that their moves are at least as good as the recommended one, and that this probability equals their probability of winning at the end of this move.


Like GNU Go, Pachi is only as good as its heuristic algorithm, and if it can't see as far ahead in the game as the professionals can, then the probability it predicts will not be illuminating.  Indeed, comparing the GoGameGuru's notes on which moves were brilliant and which were mistakes to Pachi's did not yield any noticeable correlation.  In fact, Pachi seemed to think that black resigned when he was in fact coming back!

Figure 6:  Pachi analysis of Junghwan vs. Yue.  Major predicted turning points in the game are noted.  For instance, from moves 123 to about 182, white was pulling ahead.  After move 182, black was coming back in the game according to Pachi, but resigned at the end of move 238.  Compare this to the analysis given at GoGameGuru.  Pachi was run with 1 million simulations per move and using the extra pattern files.

Pachi's analysis of the 9d game is understandably flawed, as it is not as strong as these players.  Still, the analysis by Pachi shows an important point:  the value of a move depends greatly on your definition of value.  If you care about expected point value then, indeed, an early game move is much more valuable than a late game move.  On the other hand, if you care about winning or losing then the game can certainly come down to a matter of a few points, and those few points can make a world of difference regardless of when they are secured.  The professional game analyzed in Figure 6 changed hands no fewer than three times:   twice in the mid-game, and once again at the end.  If I had a lot of spare processor cycles, it would be interesting to perform this analysis with Pachi on a large number of games and explore the distribution of points where the lead player changes hands.

This analysis may have raised more questions than answers, but I did learn a few things about computer Go and human nature:

• No AI can transcend its heuristics.  The AI will relentlessly play the move it sees as most profitable at every turn, whereas human players who know they are behind will tend to take a gamble to try to get back into the game, then resign if it fails.
• Whether or not there are diminishing returns in Go depends on your definition of value:  if you consider value as the number of points secured per move, then the first dozen moves of the game are worth about 10 points apiece, and any move after the 200th is worth perhaps one.  If you consider the value of a move as whether or not you can win the game with it, that could happen at any time.
• Komi does not appear in the plot of diminishing returns.  While all games tend to fall within a few points of the value curve, no game is composed entirely of average moves.

Thanks to Andrew Jackson and Chris Gaiteri for illuminating conversations on this topic!

The Rescue Mission

The recent US Government Shutdown came at great expense to the American people.  One of the side effects was that our national parks were shut down for two and a half weeks.  Ordinarily this is merely an inconvenience, but in my case it was a serious problem:  the Sunrise area closes on October 15, and the shutdown meant that my pinhole cameras would be irretrievable until next Summer.

... or would they be?  Benson suggested that we could boldly hike up from the White River campground and rescue the cameras in an epic 9-mile, 2500-ft elevation change day hike.  And so the rescue plan was born.  Remarkably, all of my cameras were still intact and where I left them and had not been found by curious or vigilant hikers.  A few of the results came out looking great, but I learned a few more lessons:

• The pinhole really should be as small as possible for a sharp image.  If a camera is to be left out for months or longer, a very small sewing pin will suffice.
• If the can is mounted vertically, then the pinhole should be on the cylindrical edge of the can and near the top of the can as it is mounted.

  

  The pinhole should be near the top of the can assuming the can is mounted vertically.

• Ideally, a subject should either have extreme color variation, be shiny, or be partially transparent.  The shadow of the subject should hit the can directly for part of the day.

Here are the successful photos:

Taken from the base of a tree on the Sourdough Ridge trail, exposed June 30-Oct 26 2013.

Camera from a dead tree on a rock outcropping.  Exposed June 30-Oct 26 2013,

Taken from behind a stump.  Exposed June 30-Oct 26 2013.

Thanks to Benson for challenging Simiao and I to undertake this daring rescue.  He took some photos of his own that you might enjoy.

Mission successful!

I Am Now Engaged

I asked Simiao to marry me on Sunday morning after breakfast, and she said yes!  This is really important to me, but at the same time not particularly surprising.  We'd been together for 3 years, 1 month and 1 day by her count.  I'd consulted with her about her favorite designs and stones when ring shopping.  We'd talked about a future together.  By the time I asked her, her answer was a foregone conclusion.

 You wouldn't have known that from how nervous I felt going in.  When I was on my way to the airport to pick her up, and when I was driving up to The Inn on Orcas Island for our weekend getaway, I couldn't drive at a constant speed because my feet were shaking nervously.  I didn't sleep at all the night before, and if I did start to doze, I had nervous dreams like this one:

An actual dream I had the night before I proposed to Simiao.  Proof that my imagination hates me.

Finally, at breakfast, I couldn't finish the delicious eggs Florentine and my hands were shaking badly enough that I could not hold my teacup steady.  I did have the clever idea to wait until the end of the meal to propose because I didn't want Simiao to cry and ruin her makeup and have to sit through the meal that way, and it's good that I did because no sooner did I take the box out of my pocket than she started to cry.  Her crying made me forget exactly what I wanted to say, which I had carefully rehearsed about a thousand times.

What I intended to say.

What was actually said.

Simiao, do you remember what I said I wanted from a relationship when we first met? I said I wanted compromise, patience, and reciprocity.   You gave me all of those things. On top of that, you are generous,  brilliant, hardworking honest, loving, adventurous, and every day you challenge me to be a better person and a better partner. I love you, and if you feel the same way, then will you marry me?

Sweetheart, don't cry yet, I haven't even started! Simiao, do you remember what I said I wanted from a relationship when we first met?I said I wanted compromise, patience, and reciprocity.   [Hug break] You gave me all of those things. On top of that you are generous, brilliant, ... and a bunch of other things I can't remember right now because I'm so nervous... every day you challenge me to be a better person and a better partner. I love you, and if you feel the same way, then will you marry me?

Thankfully, she forgave me for forgetting my lines and said "Yes" anyway.

Actually, I think the hardest part of the road to engagement was coming to a better understanding of love.  A long time ago I was at a friend's bachelor party and he was having a conversation with a much, much older gentleman.  The older gentleman was talking about how lucky my friend was to be in love his fiancee.  The older gentleman related that he had never actually loved his wife who he had been with for decades and with whom he had several children.  The possibility that this could actually happen to a person was terrifying to me, and because of this I spent years carefully examining every romantic relationship I had:  Do I actually love this person?  How do I know if I actually love this person?  What if this feeling isn't actually love?  What if I love someone else more?  How do you even compare that?  This is a fruitless line of thought.

The table where I proposed to Simiao.  The best thing about this table was that since I was facing away from the rest of the room, I didn't have to see their eyes on me.

I've heard it said that people spend a lifetime looking for the feeling they get the first time they fall in love.  I've come to believe that this is indeed true.  People also spend a lifetime looking for the feeling they get the second time, the third, the fourth, et cetera.  I have learned that every person you ever love, be it your parents, your brother, your best friend, or a romantic interest, you will love in a different, unique and irreplaceable way.  Thankfully, loving one person romantically isn't mutually exclusive with loving any number of people Platonically.  Your family will still be there, your friends will still be there, and your partner will understand that it is not necessary or desirable that you should share every single hobby and interest and that these other people are an essential part of your life as well.  This simple realization quieted my concerns about whether the way I felt about Simiao was right and let me instead focus on why, as I should have been all along.

Why is Platinum More Expensive than Gold?

During a discussion at dinner today, I asked a question that seems silly and naive:  why is platinum more expensive than gold?  The answer, I think, is interesting and surprisingly complicated.

I read an article recently that said that the majority of the universe's gold and platinum originates from neutron star collisions, and in fact that 7 to 10 times more platinum comes from these collisions than gold.  Figure 1 shows a reproduced and modified figure from the article where they show the expected mass fraction ejected of a variety of atomic mass numbers.  It's noteworthy that gold is stable only at mass number 197, whereas platinum is stable at mass numbers 194, 195 and 196.  Roughly 1/3 of the platinum around today is atomic mass 194, 1/3 is 195, about 1/4 is 196, and most of the rest is atomic mass 198.

Figure 1:  Adapted from Goreily et. al. (2011).  Mass fractions of heavy elements ejected from neutron star collisions.  This is believed to be the major source of heavy elements in the universe.

If we assume that all of the ejecta at each mass number ends up being the corresponding element, then summing the mass fractions for platinum 194, 195, 196 and 198 in figure 1 we see that the mass fraction of platinum ejected from the collision of two neutron stars is about 0.015, and the mass fraction of gold ejected is 0.002.  That means that about 7.5 times more platinum coming out of our collision than gold.

Now our chunks of platinum and gold hurtle out of a gravity wave inducing neutron star collision into space and eventually land in our solar system in the form of meteors.  There's no reason to believe that platinum and gold have separated out significantly on their way to Earth since the abundance of these elements on Earth are 1.9 micrograms/gram for platinum and 0.16 micrograms/gram for gold--so there is roughly 11.8 times more platinum than gold in our planet as a whole by mass.

However, the platinum in the core and the mantle is all but inaccessible to us.  The abundance of platinum and gold in the crust on the other hand is roughly equal at 0.0037 parts per million for platinum and 0.0031 parts per million for gold.  It is still not worth mining either unless some natural process concentrates it, and it seems that there must be fewer such natural processes that lead to the concentration of platinum since only 179 tons of platinum were mined in 2012 compared to 2,700 tons of gold.  For instance, gold deposits form at fault lines when rapid pressure changes during earthquakes cause dissolved gold to precipitate from water underground.  I could not find any articles on natural mechanisms for concentration of platinum.

Finally, there is human history working in favor of gold.  Gold has been known and collected for as long as recorded history, whereas platinum was only recently discovered in the mid-1750s.  Nearly all of the gold that humans have ever collected is still with us in one form or another, and it is estimated that all of the gold that humans have ever possessed equals about 283,000 metric tons, compared to only about 6,000 metric tons of platinum.

So, thanks to geology and human history, we have gone from platinum being 7.5 times more common than gold in neutron star collisions to being substantially scarcer than gold in our possession.  Without considering global demand, it's still fair to say this scarcity in supply is why platinum is more expensive than gold.

Folding Kinetics of Riboswitch Transcriptional Terminators and Sequesterers

A golden buprestid found near Port Angeles
sparkles like an exotic jewel.

A paper that I started as a graduate student, Folding Kinetics of Riboswitch Transcriptional Terminators and Sequesterers, was recently published in Entropy.  I won't reproduce the paper here, but instead I wanted to give a layman's explanation of what we found.

A riboswitch is a piece of RNA that serves both as a detector of some kinds of molecules and a switch to turn a gene's expression on and off.  For example, bacteria might be able to consume a certain kind of nutrient.  If the nutrient was found in the bacteria's environment, it would turn on a gene to make some proteins that can metabolize the nutrient.  The bacteria could use a riboswitch to sense the nutrient and to turn on the gene to digest it.

Some riboswitches work at the time of gene transcription, and work by stopping the RNA polymerase from completing the messenger RNA.  This process is called transcriptional termination.  Obviously, these riboswitches must perform their task quickly, because the RNA polymerase is able to make a gene on the timescale of seconds.

Other riboswitches work at the time of gene translation, and work by preventing a ribosome from binding to the messenger RNA and making the related protein.  We call these sequesterers.  The messenger RNA can be present in the cytoplasm for minutes or hours, so these riboswitches have a much longer timescale on which they may perform their task.

All riboswitches, like proteins, must fold into a particular shape in order to perform their tasks.

Using the open-source ViennaRNA software package, we simulated the folding of thiamine pyrophosphate riboswitches that use either the mechanism of transcriptional termination or sequestration to control their related genes and study the time it takes each type of riboswitch to fold into its functional shape.  We find evidence that the transcriptional terminators, which must operate on a faster timescale than sequesterers, are naturally selected to fold more efficiently.

Moonrise

Piper's Bellflower, growing in the
Alpine meadows at Hurricane Ridge.

I was at the Olympics this weekend with a friend, and on Saturday night after dark we went out with our cameras to try some long exposures.

It was dark there!  Even though we could clearly see the city lights from Port Angeles, it was so dark that the plane of the Milky Way was obviously visible in the night sky.  Feeling ambitious, I decided to take a very long 30 minute exposure with an inspired shot.  There was a teardrop camper parked on his parents' properly, resting idyllically under some fruit trees with the mountains in the background.  I decided to brightly light-paint the mechanical teardrop camper with an LED flashlight, and then light paint the underside of the trees more gently with the golden hue of an incandescent.  12 minutes into the shot, Nature decided to step in and paint everything else as the moon rose over the Olympics.  The result is one of my favorite photos I've ever taken.  Thanks to Benson for his assistance in light painting this shot!

30 minute exposure, ISO 100, f/3.5.  Light painted.  No photoshopping.  

An Arduino Time-Lapse Camera Using ArduCam

While experimenting with my pinhole cameras, I did a lot of thinking about capturing and displaying the passage of time.  Day and night, the change of seasons, sunrise, sunset, moonrise, moonset, tides, rush hour, busy times at restaurants, even life and death marks the passage of time.

There are plenty of commercially-available time-lapse photography devices.  These require either an AC power source, a solar panel or a beefy battery, expensive photography equipment, and are large and easy to spot.  Between the size and the expense, this strongly limits the duration of time lapse I would be able to take even if such a device wasn't prone to being stolen by the first philistine that came across it.  My goal is to make the smallest, most energy efficient and least expensive camera possible so that I am free to set them everywhere and see what the passage of time shows me.

To do this, I decided to give ArduCam a try.

Actually, I found ArduCam pretty disappointing and difficult to use for a few reasons:

• The open source libraries don't use any modern version control system like GitHub.  They're just a few files.  What's more, they fail to compile under Linux without changing the #include statements to correct for case-sensitivity.
• While the ArduCam website shows full-resolution images pulled from "supported" camera modules, the ArduCam Rev. B shield is unable to take bitmap images greater than 320 by 240 pixels because it has only a 3 megabit buffer.  For cameras with on-board JPEG compression it is able to take higher-resolution images, but they come out looking fuzzier than a Georgia peach because they must be made to fit in the buffer.  If these images were indeed taken with an ArduCam shield, they weren't done with any code made available on their website.
• The first "supported" camera I bought, the MT9D111, failed to take any worthwhile picture at any resolution.  I was only able to get it working with the OV2640 module.

Sample image taken with the "supported" MT9D111 camera using an example from the open-source ArduCam code.

So, the ArduCam was a bit of a let-down.  It is actually pretty impressive that someone figured out how to hack together a camera that interfaces with an Arduino, but it's not particularly useful.  The image size is pathetically small and the power draw is substantial (I'm able to take about 370 images on 4 AA batteries).  It may be useful for some applications, but quality time-lapse photography is not going to be one of them.

Let's take a look at my camera, my code, and the results.

My ArduCam

My camera uses the following components:

• Arduino Uno Rev. 3
• ArduCam Rev. B Shield
• OV2640 Camera Module
• 2GB MicroSD Card
• 4 AA batteries

Assembly is positively trivial.  Everything just fits together.  Build time is under a minute.

Note that while the ArduCam board can be made to work with the Arduino Mega, it requires some rewiring because the pinouts are not exactly the same.  The power efficiency could have been improved somewhat with a DC step-down buck converter, but I decided against doing this because even if the power efficiency was greater the image resolution was unacceptable.

An image taken with the OV2640 out an office window at Google Seattle.

The first iteration of my code simply took a picture, then waited a minute using delay before taking another, repeating until the camera ran out of battery.  This managed to take 364 bitmap images until it ran out of juice.  The second iteration of my code made use of the Sleep_n0m1 library to place the Arduino in sleep mode and wake it up each minute.  I had hoped that this would improve battery life substantially, but instead it managed only to take 370 images before running out of battery.

I assembled the time-lapse photos into a video using the following command with avconv on Linux:

avconv -f image2 -i %08d.BMP output.avi

Overall, this was an enlightening exercise but it's clear that if I want a very long-term and reasonably high-quality time lapse photo solution, the platform for that is not going to be ArduCam.

More Pinhole Photography from Mt. Rainier

I pulled 4 of my original 6 pinhole cameras from Mt. Rainier's Sunrise Area last weekend.  The results confirmed some follies of my original design and placement strategy:  First, the camera should be mounted vertically like the soda can sits.  Mounting the camera horizontally does not give the massive depth-of-field effect that I expected it to.  Second, the pinholes were way too large.  1mm diameter pinholes are way too big.  Finally, I underestimated the vigilance of passers-by.  The mountain was only open to visitors for three days total while my cameras were there, and one was crushed by some curious tourist during one of those three days.  Only one of the four cameras that I retrieved gave what I would call a worthwhile shot.  One thing that I like about it is that you can see the first few snowfalls:  horizontal bars show the ever-increasing level of the snow with the trees disappearing behind it over time!

Pinhole photo from Mt. Rainier's Sunrise area.  1mm pinhole, can mounted horizontally, and exposure lasted from October 6, 2012 to June 29, 2013. 

Arduino Scalable Single-Stage Coilgun

In my earlier post where I built an Arduino Laser Tripwire, I mentioned that I was going to use this as a component to a later project.  I've built a scalable, single-stage coilgun that uses inexpensive components and a relatively tame 50VDC.

The premise of a coilgun is simple:  a ferromagnetic or paramagnetic projectile is attracted towards any strong magnetic field it encounters.  By switching on a strong magnetic field inside a solenoid, we can attract the projectile into the coil of wire.  When the projectile is inside the wire, the field is switched off and the projectile continues on the path it was following as it was sucked into the field.

This prototype has only a single stage, meaning that only a single solenoid accelerates the projectile; However, it can easily be scaled up.  By placing another stage just like it in the path of the projectile, we can accelerate the projectile faster and faster.  The projectile will break the laser beam for the next unit, then the magnetic field in the next solenoid will be turned on thus accelerating the projectile further.

I can achieve this multistage coilgun by placing a clear plastic barrel down the center of my solenoids, then shining the laser through the barrel.

My charging circuit, a Delon voltage doubler.

My charging circuit is a simple Delon voltage doubler.  The voltage doubler uses a 12VA transformer to convert the 120V AC from a normal US wall outlet to 24V AC.  The capacitors only need to be 24V, but I happened to have 35V capacitors on hand.  To protect my Arduino from any reverse bias that might be introduced by the relay coil, I include a 1N4937 diode in my design for protection.

My Arduino laser tripwire module., modified from my earlier design.

I have modified my Arduino laser tripire module a bit for compatibility with my trigger circuit.  I need a 1N4937 diode to prevent the voltage from my main capacitor from flowing to ground through the 100 ohm resistor on the trigger circuit.  The indicator LEDs are all optional, and power draw on my Arduino could be reduced by removing them.

The firing module for my prototype coilgun.

The firing circuit is quite spartan, dominated by a large electrolytic capacitor and a cheap 2N6507G SCR.  The 2N6507G can withstand a surge current of 250A but costs only 66 cents to purchase, making it an ideal centerpiece for my firing circuit.  To simplify things further, I use an entire quarter-pound spool of 16AWG magnet wire for my solenoid.  No winding was necessary:  I simply purchased the spool, found both ends of the wire, sanded the insulating lacquer off, and crimped on terminals.  I measured its inductance at 185 microhenries.  To be absolutely sure to protect my capacitor from any reverse bias that might be introduced, I have a 1N4937 protection diode across both the solenoid and the terminals of the capacitor.

Complete schematics for my prototype, generated with KiCad.

Before getting to the demonstration, I will share the source code that I uploaded to my Arduino Uno.  This source is similar to that which I included in my previous post, except I have modified it in two ways.  First, it opens the power supply relay at the same time that the SCR is triggered.  Second, it includes a charge signal (output 10) as well as a tripped signal (output 11).

int ledPort = 13; int laserPort = 12; int tripPort = 11; int notTripPort = 10; int timerToggle = 1000; int timerCount = 0; boolean timerState = false; int onLevel = -1; int offLevel = -1; int currentLevel = -1; boolean tripped = false; void setup() { pinMode(ledPort, OUTPUT); pinMode(laserPort, OUTPUT); pinMode(tripPort, OUTPUT); pinMode(notTripPort, OUTPUT); digitalWrite(tripPort, LOW); digitalWrite(notTripPort, HIGH); // Check the state of the phototransistor with the laser on // and off. digitalWrite(laserPort, LOW); delay(1000); offLevel = analogRead(A0); digitalWrite(laserPort, HIGH); delay(1000); onLevel = analogRead(A0); } // An alive signal that appears on the arduino, // just to let me know the program is running. void timer() { timerCount++; if (timerCount == timerToggle) { timerCount = 0; timerState = !(timerState); if (timerState) { digitalWrite(ledPort, HIGH); } else { digitalWrite(ledPort, LOW); } } } void loop() { delay(1); timer(); if (!(tripped)) { currentLevel = analogRead(A0); if (currentLevel < onLevel - (onLevel - offLevel) / 10) { tripped = true; digitalWrite(tripPort, HIGH); digitalWrite(notTripPort, LOW); } } }

Source code for my coilgun, as uploaded to my Arduino Uno.

Finally, you may check the YouTube video below to see how it works!

Pinhole Camera, Mark 3

The underside of a limpet.

I pulled a couple more of my pinhole cameras from Magnolia Park the other day.  I've gotten better at hiding them!  This time two of three were still where I left them, and one was so well hidden that even when three of us were standing with our heads less than two feet from it we still took five minutes to find it.

These pictures were plagued by a problem from my original design:  the pinhole was simply too large.  The results were a little bit fuzzy, and the effects of condensation and mist rolling in from the Puget Sound are apparent.  Further, the summer sun was cut off at the bottom of the can.  These are problems that I hope to fix in my future pinhole camera projects.  In addition to using a smaller hole perhaps half a millimeter in diameter, I will place the hole higher up in the can.  In this manner, the can mounted vertically with the hole near the top will be less prone to cutting off the sun trails in the summer.  Further, I will include some silica gel inside the can to try to absorb some moisture before it can condense.  I will also experiment with a small amount of saran wrap or clear plastic over the pinhole to try to keep any moist air out.

Pinhole camera mounted among some trees and overlooking Puget Sound at Magnolia Park facing roughly Southwest.  Black and white satin finish paper, 1mm diameter pinhole, exposed from March 3 - June 17 2013.

More Lessons from the Pinhole Cameras

With some help from a friend who lent me the roof of his Apartment building, we managed to take my best pinhole camera exposure to date.  It's still not great, but I'm pretty new to the art form and it's going to take some practice to get right.  This one was exposing for about 5 months from January to June 2013, facing South.  About half the frame is taken up by the roof of his building, and the rest should have looked like the city skyline, but it came out quite blurry.  The instructions I followed online for making them suggested a 1mm diameter hole, but I think that was misguided.  1mm is the diameter of a small nail, and everything came out fuzzier than a Georgia peach.  I think using an actual pin to make the hole as recommended in these instructions would lead to much better results in the future!  Also, after some experimentation with horizontal mounting, I would say that those shots were disappointing.  Be sure to mount your drink-can camera vertically (the way the can would sit if it was on the table) for best results.

In a previous blog post I suggested that the photo paper was forgiving to moisture, but the results of this image leads me to believe that in fact the fine details are washed away by any water or condensate that gets in, leaving only the bold sun-trails.

I've got a lot more of these in the works!  For now, enjoy my first kind-of decent pinhole camera photo.

The roof of an apartment building North of Lake Union, facing South over the city of Seattle.  1mm diameter pinhole, exposed on resin-coated 5"x8" black and white photo paper.  January-June 2013.

It can be improved quite a bit with GIMP, though.  If I invert the colors then take a look at the color curves, I can select a curve to improve the dynamic range of my image.

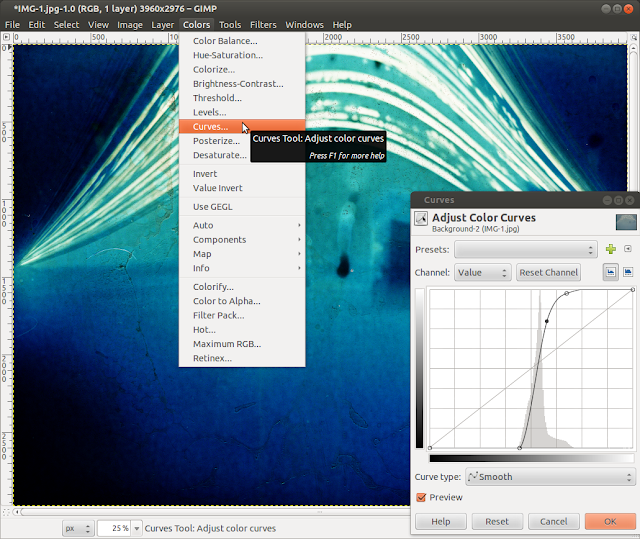Improving the dynamic range of my pinhole camera picture using the magic of GIMP.

The end result is certainly a lot more interesting to look at than the original!

The same image as above, with colors inverted and dynamic range improved in GIMP.

Even More Betting Strategies at the DotA 2 Lounge

My previous post, Betting Strategies at the DotA 2 Lounge, is to date the most popular post I have ever made to this blog.  It's popular enough that I decided that I can do better!  There were some unanswered questions in the original post:  What are the most overrated and underrated teams?  Are people who bet rares more prudent with their bets than uncommons or commons?  Would the inclusion of all of the historical data from the DotA 2 Lounge affect my results at all?  I scraped all of the data from the first 400 matches at the DotA 2 Lounge using wget in a shell script, and threw out all matches where the bets were either cancelled or where the data was incomplete.  This left me with data on 334 historical matches from which to draw conclusions, including the odds on commons, uncommons and rares separately.  Basically, this analysis will give far better confidence than my previous one, and allow me to ask questions that I was previously unable to.

Let's start again by examining the crowd favor of the winning teams.  Just as in Figure 1 of my previous post, I expect to see this plot skewed to the right if the betting crowd has any ability at all to pick the winning team.

Figure 1:  Histogram of crowd favor of the winning team.  Clearly, the crowd usually favors the winning team (everything to the right of x=0.5 on the graph) and chooses correctly about 2/3 of the time.  

Indeed, Figure 1 shows that the crowd usually picks correctly and favors the winning team about 2/3 of the time.  Remember, though, that the goal of the gambler is not to pick correctly:  the goal is to profit!  First, as in my previous post, I need a control group to compare everything else to.  I will start by getting a handle on how well I will do over time if I flip a coin and bet randomly.  I will put 1 common, uncommon or rare on the team determined by the coin flip and chart my behavior.

Figure 2a:  Number of commons won by random coin flip in the first 334 matches at the DotA 2 Lounge.  Average = -2.7 items, Standard deviation = 19.6 items.

Figure 2b:  Number of uncommons won by random coin flip in the first 334 matches at the DotA 2 Lounge.  Average = -4.0 items,  Standard deviation = 19.4 items.

Figure 2c:  Number of rares won by random coin flip in the first 334 matches at the DotA 2 Lounge.  Average = -3.4, Standard deviation = 19.6 items.

Contrary to my original study with a smaller data set, Figure 2 gives a more flattering view of the wisdom of the crowd.  Betting randomly appears to be a bad idea, paying out at about 0.99:1 over 334 matches.  This is basically the behavior we'd expect in a system where the entire betting public has good information on what's going on.

Let's find out what happens if I bet 1 common, 1 uncommon, and 1 rare on the crowd favorite based on the payout per item for every match.  If there is no crowd favorite (1:1 odds), then I will abstain from betting.  I will track the behavior of my winnings over the 334 matches that had complete data and that were not canceled.

Figure 3a:  Behavior of betting 1 common on the crowd favorite for each of the first 334 complete, non-canceled matches.

Figure 3b:  Behavior of betting 1 uncommon on the crowd favorite for each of the first 334 complete, non-canceled matches.

Figure 3c:  Behavior of betting 1 rare on the crowd favorite for each of the first 334 complete, non-canceled matches.

Figure 3 shows the behavior of a hypothetical scheme where I bet 1 common, 1 uncommon, and 1 rare on the crowd favorite of each match through the history of the DotA 2 Lounge.  My hypothetical winnings fluctuate around 0 and never come close to the 40-item mark that is necessary in order to reach statistical significance.  This is another mark of a rational crowd:  going with the crowd neither makes you significant gains nor losses over time.  

Now let's try the same experiment, except this time I'm always going to bet against the crowd.  Is this a winning strategy?

Figure 4a:  Behavior of betting 1 common on the underdog for each of the first 334 complete, non-canceled matches.

Figure 4b:  Behavior of betting 1 uncommon on the underdog for each of the first 334 complete, non-canceled matches.

Figure 4c:  Behavior of betting 1 rare on the underdog for each of the first 334 complete, non-canceled matches.

Figure 4 shows that betting on the underdog is also not a great long-term strategy.  Like betting with the crowd, it never approaches the 40-item mark we need in order to reach statistical significance.  So, it seems that the crowd is actually pretty decent at picking the proper odds of winning at the DotA 2 Lounge after all.  Reassuringly, I never indicated that betting with the crowd or against it was a statistically significant improvement over random betting in my previous post.  There is a claim, however, that was statistically significant:  that betting for the left column is a losing strategy over time, and betting for the right column is a winning strategy over time.  In my previous study, these actually were at the border of statistical significance.  Given the larger data set, will these assertions be supported?

Figure 5a:  Behavior of always betting 1 common on the team in the left column.	Figure 5b:  Behavior of always betting 1 common on the team in the right column.
Figure 5c:  Behavior of always betting 1 uncommon on the team in the left column.	Figure 5d:  Behavior of always betting 1 uncommon on the team in the right column.
Figure 5e:  Behavior of always betting 1 rare on the team in the left column.	Figure 5f:  Behavior of always betting 1 rare on the team in the right column.

Figure 5 does seem to show a sustained trend towards gamblers betting favorably towards the team in the left column, and indeed there seem to be times when this could be construed as significant.  In particular, the peak around match 180 in 5b, 5d and 5f seems to be fairly significant given the number of matches played thus far.  Fast forward to today, though, and the crowd has since rectified its irrational ways.  Whether you're betting commons, uncommons or rares in the right-column strategy, you are nowhere near statistical significance today.  

I plan on following up with another post on the most overrated and underrated teams, but first I want to correct my conclusions from my original post.  Upon gathering more data from the DotA 2 Lounge, my previous conclusions are definitely affected:  betting for the right column may have been a statistically significant good strategy in the past, but it is not anymore.   The strategies of flipping a coin, always betting with the crowd, and always betting for the underdog all remain statistically insignificant.  

I definitely made an amateur mistake in overstating the trends I did find.  It is not correct to advocate a strategy (such as flipping a coin or betting for the underdog) that is not statistically significant--I've learned from this mistake, and will not repeat it in the future!

If you'd like to gather your own data from the DotA 2 Lounge and perform your own analysis, I've made the scripts I used available.  Please feel free to use the data you gather for any purpose you like.  If you decide to make your own blog post about the trends you find, let me know and I'll link you from here!

Update:  If you enjoyed this post, you may also like my more recent post: What is the Most Underrated DotA 2 Team?